
INDICE
Parte 1: Introduzione.
Parte 2: Fasi, variabili, operatori e software.
Parte 3: Tipi di dato, direttive e primo programma.
Parte 4: Tipi di formato, prinft e scanf.
Parte 5: Istruzioni condizionali e di iterazione.
Parte 6: Funzioni e progetti su più file.
Parte 7: Puntatori e passaggio dei parametri.
Parte 8: Array, stringhe e strutture.
Parte 9: Gestione file: file di testo.
Parte 10: Gestione file: file binari.
Parte 11: Allocazione dinamica della memoria.
Parte 12: Creare ed utilizzare le liste nel C.
Parte 13: Algoritmi di ordinamento di Array.
Parte 14: Esercizi sul linguaggio C.
- Naive sort: molto semplice, ma poco efficiente;
- Bubble sort: la più usata, perché abbastanza semplice e abbastanza efficiente;
- Insert sort: non facilissima, ma più efficiente della bubble sort;
- Merge sort: di difficile comprensione, ma molto efficiente;
- Quick sort: di difficile comprensione, ma la più efficiente.
Esaminiamole ora insieme una alla volta molto rapidamente, poichè vi do poi la possibilità di scaricarle tutte insieme raccolte in un unico file; prima però bisogna definire altre tre funzioni, utili ai fini dell’ordinamento:
void assign(Element *lvalue, Element rvalue);

void swap(Element *e1, Element *e2);

int compare(Element e1, Element e2);

La Naive sort è l’algoritmo di ordinamento più facile; in sostanza prima assume come massimoil primo elemento di un array (o struttura, o lista), poi si scandisce l’array e, se si trova un elemento maggiore del max attuale, lo si assume come nuovo massimo, memorizzandone a questo punto la posizione.Bubble sort
La Bubble sort è l’algoritmo di ordinamento più usato in assoluto, e secondo me è quello migliore e più intuitivo da usare; la Bubble sort opera per “passate successive” sull’array:
- Ad ogni ciclo confronta gli elementi a due a due, eventualmente scambiandoli se non sono nell’ordine che si desidera;
- In sostanza, ad ogni iterazione quindi l’elemento più grande si trova sempre in fondo alla parte di array considerata.
Insert sort
Solitamente per ordinare un array “basta” costruirne uno nuovo ordinato con gli stessi elementi; invece con la Insert sort non è assolutamente necessario costruire un secondo array, in quanto le operazioni per ordinare un array possono essere svolte direttamente infatti sull’array originale.
Merge sort
La Merge sort produce sempre due sub-array di uguale grandezza; in sostanza:
- Spezza l’array in due parti di uguale dimensione;
- Ordina queste due parti separatamente, procedendo per ricorsione;
- Infine fonde insieme i due sub-array in modo da ottenerne uno unico ordinato.
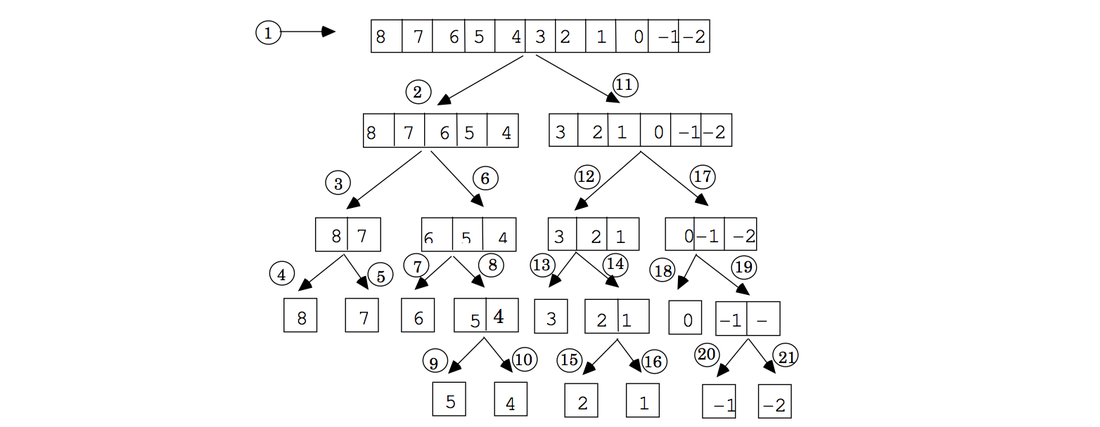
Come la Merge sort, la Quick sort suddivide il vettore in due sotto-array, delimitati da un elemento “sentinella” (un pivot); il pivot viene poi spostato ricorsivamente in modo da raggiungere l’obiettivo, che e’ quello di avere nel primo sotto-array solo elementi minori o uguali al pivot, e nel secondo sotto-array solo elementi maggiori. Quindi procede così:
- Si determina un pivot (ad esempio pivot = a[dim-1]);
- Si scandisce il vettore dato mediante due indici: i, che parte da 0 e procede in avanti, e j, che parte da dim-1 e procede all’indietro;
- Poi procede ad una scansione in avanti: ogni elemento a[i] viene confrontato con il pivot; se a[i] > pivot, la scansione in avanti si ferma;
- Se la scansione in avanti si ferma, si procede a quella indietro: ogni elemento a[j] viene confrontato con il pivot; se a[j] < pivot, la scansione in indietro si ferma e l’elemento a[j] viene scambiato con a[i];
- Poi si riprende con la scansione avanti, indietro, … Il tutto si ferma quando i == j. A questo punto si scambia a[i] con il pivot;
- Alla fine della scansione il pivot è collocato nella sua posizione definitiva;
- L’algoritmo è ricorsivo: si richiama su ciascun sotto-array fino a quando non si ottengono sotto- array con un solo elemento;
- A questo punto il vettore iniziale risulta ordinato!
A questo punto vi metto a disposizione qui da scaricare tutti gli algoritmi di ordinamento, adatti per ogni sorta di struttura: array, struct, liste; basterà infatti solamente cambiare le operazioni “swap, compare e assign” e la definizione di Element per adattarle:
| ordinamento.zip |
Dottore in Ingegneria Informatica.
Contattatemi sui miei Social Network e sul mio Sito personale per collaborazioni, proposte di lavoro e altre informazioni!







